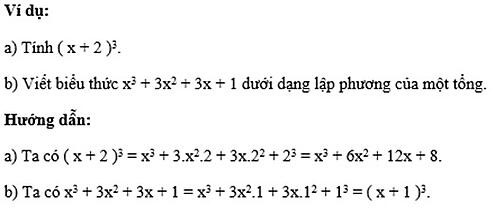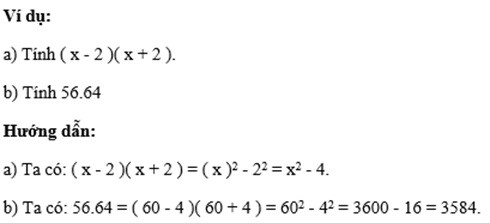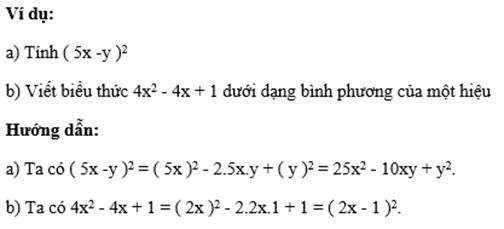Công Thức, Bài Tập Về 7 Hẳng Đẳng Thức Đáng Nhớ Và Các Hằng Đẳng Thức Mở Rộng

Hẳng đẳng thức là một trong những kiến thúc toán quan trọng với hầu hết các bấc lớp cấp hai. Nhớ lại các công thức về 7 hằng đẳng thức đáng nhờ cùng Review Điện Thoại với các hằng đẳng thức mở rộng cấp 2, 3 và giải thêm một số bài tập về các hằng đẳng thức mở rộng, đáng nhớ nhé!
Xem thêm >> [Update] Chú Trọng, Trú Trọng Là Gì? Đâu Mới Là Cách Viết Đúng?
7 Hằng đẳng thức đáng nhớ

Bình phương của 1 tổng
Bình phương của 1 tổng bằng bình phương của số thứ 1 cộng với hai lần tích số thứ 1 và số thứ 2, sau đó cộng với bình phương của số thứ 2.
Ví dụ:
a) Tính ( a + 3 )2.
b) Viết biểu thức x2+ 4x + 4 dưới dạng bình phương của một tổng.
Hướng dẫn:
a) Ta có: ( a + 3 )2= a2+ 2.a.3 + 32= a2+ 6a + 9.
b) Ta có x2+ 4x + 4 = x2+ 2.x.2 + 22 = ( x + 2 )2.
Bình phương của một hiệu
Bình phương của một hiệu bằng bình phương số thứ 1 trừ đi hai lần tích số thứ 1 và số thứ 2. Sau đó trừ đi bình phương số thứ 2.
Hiệu hai bình phương
Hiệu hai bình phương bằng tích tổng hai số đó nhân với hiệu hai số đó.
Lập phương của một tổng
Lập phương của một tổng bằng lập phương số thứ 1 cộng với 3 lần tích bình phương số thứ 1 nhân với số thứ 2 cộng với 3 lần tích xố thứ 1 nhân với bình phương số thứ 2 sau đó cộng với lập phương số thứ 2.
Lập phương của một hiệu
Lập phương của một hiệu bằng lập phương số thứ 1 trừ đi 3 lần tích bình phương số thứ 1 nhân với số thứ 2 cộng với 3 lần tích xố thứ 1 nhân với bình phương số thứ 2 sau đó trừ với lập phương số thứ 2.
Ví dụ :
a) Tính ( 2x – 1 )3.
b) Viết biểu thức x3– 3x2y + 3xy2– y3dưới dạng lập phương của một hiệu.
Hướng dẫn:
a) Ta có: ( 2x – 1 )3
= ( 2x )3 – 3.( 2x )2.1 + 3( 2x ).12 – 13
= 8x3 – 12x2 + 6x – 1
b) Ta có : x3– 3x2y + 3xy2– y3
= ( x )3 – 3.x2.y + 3.x. y2 – y3
= ( x – y )3
Tổng hai lập phương
Tổng hai lập phương bẳng tổng hai số nhân với bình phương thiếu của hiệu thứ 1 và thứ 2.
Quy ước A2 – AB + B2 là bình phương thiếu của hiệu A – B.
Ví dụ:
a) Tính 33+ 43.
b) Viết biểu thức ( x + 1 )( x2– x + 1 ) dưới dạng tổng hai lập phương.
Hướng dẫn:
a) Ta có: 33+ 43= ( 3 + 4 )( 32– 3.4 + 42) = 7.13 = 91.
b) Ta có: ( x + 1 )( x2– x + 1 ) = x3+ 13 = x3 + 1.
Hiệu hai lập phương
Hiệu hai lập phương bằng hiệu hai số nhân với với bình phương thiếu của tổng số thứ 1 và thứ 2.
Quy ước A2 + AB + B2 là bình phương thiếu của tổng A + B.
Ví dụ:
a) Tính 63– 43.
b) Viết biểu thức ( x – 2y )( x2+ 2xy + 4y2) dưới dạng hiệu hai lập phương
Hướng dẫn:
a) Ta có: 63– 43= ( 6 – 4 )( 62+ 6.4 + 42) = 2.76 = 152.
b) Ta có : ( x – 2y )( x2+ 2xy + 4y2) = ( x )3 – ( 2y )3 = x3 – 8y3.
Xem thêm << [Share] Ẩn Dụ, Hoán Dụ Là Gì? Ví Dụ Và Cách Phân Biệt Ẩn Dụ, Hoán Dụ
Bài tập về các hằng đẳng thức đáng nhớ
Bài 1.Tìm x biết
a) ( x – 3 )( x2+ 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.
b) ( x + 1 )3– ( x – 1 )3– 6( x – 1 )2= – 10.
Hướng dẫn:
a) Áp dụng các hằng đẳng thức ( a – b )( a2+ ab + b2) = a3– b3.
( a – b )( a + b ) = a2 – b2.
Khi đó ta có ( x – 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.
⇔ x3 – 33 + x( 22 – x2 ) = 0 ⇔ x3 – 27 + x( 4 – x2 ) = 0
⇔ x3 – x3 + 4x – 27 = 0
⇔ 4x – 27 = 0
Vậy x=27/4.
b) Áp dụng hằng đẳng thức ( a – b )3= a3– 3a2b + 3ab2– b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a – b )2 = a2 – 2ab + b2
Khi đó ta có: ( x + 1 )3 – ( x – 1 )3 – 6( x – 1 )2 = – 10.
⇔ ( x3 + 3x2 + 3x + 1 ) – ( x3 – 3x2 + 3x – 1 ) – 6( x2 – 2x + 1 ) = – 10
⇔ 6x2 + 2 – 6x2 + 12x – 6 = – 10
⇔ 12x = – 6
Vậy x= -1/2.
Bài 2: Rút gọn biểu thức A = (x + 2y ).(x – 2y) – (x – 2y)2
- 2x2+ 4xy B. – 8y2+ 4xy
- – 8y2 – 6y2+ 2xy
Hướng dẫn
Ta có: A = (x + 2y ). (x – 2y) – (x – 2y)2
A = x2 – (2y)2 – [x2 – 2.x.2y +(2y)2 ]
A = x2 – 4y2 – x2 + 4xy – 4y22
A = -8y2 + 4xy
Bài 3. Thực hiện phép tính:
a) (2x – 1)3
b) (x + 4)3
c) (x – 2)2
d) (2x + 1)2
e) x3+ 64
f) 8x3– 27
Lời giải:
a) (2x – 1)3
= (2x)3 – 3.(2x)2.1 + 3.2x.12 – 13
= 8x3 -12x2 + 6x – 1.
b) (x + 4)3
= x3 + 3.x2.4 + 3.x.42 + 43
= x3 + 12x2 + 48x + 64.
c) (x – 2)2
= x2 – 2.x.2 + 22
= x2 – 4x + 4.
d) (2x + 1)2
= (2x)2 + 2.2x.1 + 12
= 4x2 + 4x + 1.
e) x3+ 64
= x3 + 43
= (x + 4)(x2 + 4x + 42)
= (x + 4)(x2 + 4x + 16).
f) 8x3– 27
= (2x)3 – 33
= (2x – 3)[(2x)2 + 2x.3 + 32]
= (2x – 3)(4x2 + 6x + 9).
Bài 4. Tính giá trị của các biểu thức A, B dưới đây:
a) A = x3+ 6x2+ 12x + 8 tại x = 48
b) B = x3– 3x2+ 3x – 1 tại x = 101
Lời giải:
a) A = x3+ 6x2+ 12x + 8 tại x = 48
Ta có: A = A = x3 + 6x2 + 12x + 8
= x3 + 3.x2.2 + 3.x.22 + 23
= (x + 2)3
Với x = 48 ta có giá trị của biểu thức A là:
A = (48 + 3)3 = 503 = 125000
b) B = x3– 3x2+ 3x – 1 tại x = 101
Ta có: B = x3 – 3x2 + 3x – 1
= x3 – 3. x2.1 + 3.x.12 – 13
= (x – 1)3
Với x = 101 ta có giá trị biểu thức B là:
B = (101 – 1)3 = 1003 = 1000000.
Bài 5. Tính nhanh
a) 222
b) 992
c) 1993
d) 1013
e) 19.21
Lời giải:
a) 222
= (20 + 2)2
= 202 + 2.20.2 + 22
= 400 + 80 + 4
= 484.
b) 992
= (100 – 1)2
= 1002 – 2.100.1 + 12
= 10000 – 200 + 1
= 9801.
c) 1993
= (200 -1)3
= 2003 – 3.2002.1 + 3.200.12 – 13
= 8000000 – 120000 + 600 – 1
= 7880599.
d) 1013
= (100 + 1)3
= 1003 + 3.1002.1 + 3.100.12 + 13
= 1000000 + 30000 + 300 + 1
= 1030301.
e) 19.21
= (20 – 1)(20 + 1)
= 202 – 12
= 400 – 1
= 399.
Bài 6. Rút gọn biểu thức:
a) A = (3x – 1)3– 4x(x – 2) + (2x – 1)2
b) B = (x + 1)3– 2x2(x – 2) + x3
Lời giải:
a) A = (3x – 1)3– 4x(x – 2) + (2x – 1)2
= (3x)3 – 3.(3x)2.1 + 3.3x.12 – 13 – 4x2 + 8x + 4x2 – 4x + 1
= 27x3 – 27x2 + 9x -1 + 4x + 1
= 27x3 – 27x2 + 13x
b) B = (x + 1)3– 2x2(x – 2) + x3
= x3 + 3x2 + 3x + 1 – 2x3 + 4x2 + x3
= 7x2 + 3x + 1.
Đừng bỏ lỡ >> [Update] Xuất Sắc Có Nghĩa Là Gì? Xuất Sắc Hay Suất Sắc Mới Đúng Chính Tả
Hằng đẳng thức mở rộng
Hằng đẳng thức mở rộng bậc 2
- (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
- (a + b − c)2 = a2 + b2 + c2 + 2ab − 2ac − 2bc
- (a – b − c)2 = a2 + b2 + c2 − 2ab − 2ac + 2bc
Hằng đẳng thức bậc 3 mở rộng
- a3 + b3 = (a + b)3 – 3ab(a + b)
- a3 – b3 = (a – b)3 + 3ab(a – b)
- (a + b + c)3 = a3 + b3 + c3 + 3(a + b)(a + c)(b + c)
- a3 + b3 + c3 − 3abc = (a + b + c)(a2 + b2 + c2 − ab − bc − ca)
- (a – b)3+(b – c)3+(c –a )3 = 3(a – b)(b – c)(c – a)
- (a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2
- (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc
- (a + b)(b + c)(c + a) – 8abc = a(b – c)2 + b(c – a)2 + c(a – b)2
- (a + b)(b + c)(c + a) = (a + b + c)(ab + bc + ca) − abc
Hằng đẳng thức bậc 4
( a + b )4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
Hằng đẳng thức bậc 5
( a + b )5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 +b5
Hằng đẳng thức dạng tổng quát
an + bn = (a + b)(an – 1 − an − 2b + an − 3b2 − an − 4b3 +…+ a2bn – 3 − a.bn − 2 + bn −1)
*Với n là số lẻ thuộc tập N
an – bn=(a – b)(an – 1 + an – 2b + an –3 b2 +…+ a2bn – 3 + abn –2 + bn – 1)
Bài tập về các hằng đẳng thức mở rộng
Bài 1: Tìm x biết
a) ( x – 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.
b) ( x + 1 )3 – ( x – 1 )3 – 6( x – 1 )2 = – 10.
Lời giải:
a) Áp dụng các hằng đẳng thức ( a – b )( a2 + ab + b2 ) = a3 – b3.
( a – b )( a + b ) = a2 – b2.
Khi đó ta có ( x – 3 )( x2 + 3x + 9 ) + x( x + 2 )( 2 – x ) = 0.
⇔ x3 – 33 + x( 22 – x2 ) = 0 ⇔ x3 – 27 + x( 4 – x2 ) = 0
⇔ x3 – x3 + 4x – 27 = 0
⇔ 4x – 27 = 0 ⇔ x = 27/4.
Vậy giá trị x cần tìm là x= 27/4 .
b) Áp dụng hằng đẳng thức ( a – b )3 = a3 – 3a2b + 3ab2 – b3
( a + b )3 = a3 + 3a2b + 3ab2 + b3
( a – b )2 = a2 – 2ab + b2
Khi đó ta có: ( x + 1 )3 – ( x – 1 )3 – 6( x – 1 )2 = – 10.
⇔ ( x3 + 3×2 + 3x + 1 ) – ( x3 – 3×2 + 3x – 1 ) – 6( x2 – 2x + 1 ) = – 10
⇔ 6×2 + 2 – 6×2 + 12x – 6 = – 10
⇔ 12x = – 6 ⇔ x = – 1/2.
Vậy giá trị x cần tìm là x= – ½
Bài 2: Rút gọn biểu thức:
A = (x – 2y).(x2 + 2xy + y2) – (x + 2y). (x2 – 2xy + y2)
Lời giải:
Áp dụng hằng đẳng thức:
a3 – b3 = (a – b).(a2 + ab + b2) và a3 + b3 = (a + b).(a2 – ab + b2) ta được:
A = (x – 2y). (x2 + 2xy + y2) – (x + 2y). (x2 – 2xy + y2)
A = x3 – (2y)3 – [x3 + (2y)3]
A = x3 – 8y3 – x3 – 8y3 = -16y3
Bài 3: Tìm x biết x2 – 16 + x(x – 4) = 0
Lời giải:
Ta có: x2 – 16 + x(x – 4) = 0
⇔ (x + 4). (x – 4) + x.(x – 4) = 0
⇔ (x + 4 + x).(x – 4) = 0
⇔ (2x + 4). (x – 4) = 0
⇔ 2x + 4 = 0 hoặc x – 4 = 0
* Nếu 2x + 4 = 0 thì x = -2
* Nếu x – 4 =0 thì x = 4
Vậy x = -2 hoặc x = 4.
Bài 4: Tính giá trị của biểu thức
A = 8×3 + 12x2y + 6xy2 + y3 tại x = 2 và y = -1.
Lời giải:
Áp dụng hằng đẳng thức ( a + b )3 = a3 + 3a2b + 3ab2 + b3.
Khi đó ta có:
A = 8×3 + 12x2y + 6xy2 + y3 = ( 2x )3 + 3.( 2x )2.y + 3.( 2x ).y2 + y3 = ( 2x + y )3
Với x = 2 và y = -1 ta có A = ( 2.2 – 1 )3 = 33 = 27.