[Toán Học] Công Thức Và Bài Tập Tính Diện Tích Hình Elip, Phương Trình Chính Tắc

Công thức tính diện tích elip, phương trình chính tắc là một trong những kiến thức hình học phức tạp, khó nhất trong tất cả các hình học khác. Dưới đây, Review Điện Thoại sẽ hướng dẫn các bạn một cách đơn nhất nhất về hình elip, phương trình chính tắc và công thức và bài tập tính diện tích hình elip.
Tìm hiểu >> Công Thức Và Bài Tập Tính Chu Vi, Diện Tích Hình Vuông Có Lời Giải
Hình elip
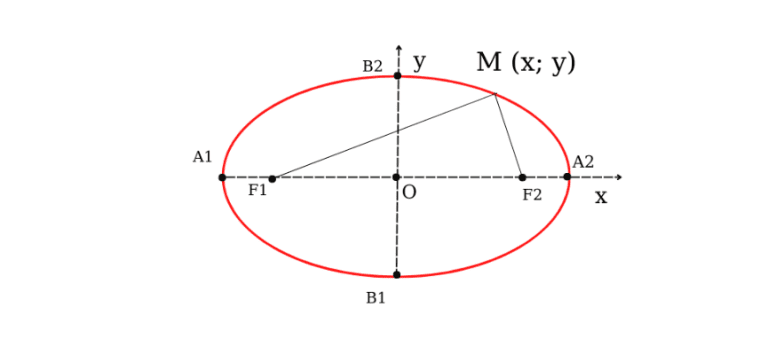
Theo định nghĩa trong toán học, hình elip được xác định bởi hai điểm cố định F1 và F2 và một độ dài không đổi 2a, với a lớn hơn độ dài F1F2. Hình elip là tập hợp các điểm M trong mặt phẳng thỏa mãn phương trình F1M + F2M = 2a. Điểm F1 và F2 được gọi là tiêu điểm của elip, và độ dài F1F2 = 2c được gọi là tiêu cự.
Một cách đơn giản để hình dung hình elip là nghĩ về việc cắt qua một hình nón hoặc hình trụ với góc lớn hơn 0. Hình tròn có thể coi là một trường hợp đặc biệt của hình elip khi cả hai tiêu điểm trùng nhau.
Công thức tính diện tích elip
Hình elip có các đặc điểm sau:
- Hình elip có hai trục đối xứng: trục lớn A1A2 và trục bé B1B2. Nửa chiều dài của trục lớn được ký hiệu là (a), còn trục bé được ký hiệu là (b).
- Hai trục đối xứng A1A2 và B1B2 là vuông góc với nhau và giao nhau tại tâm đối xứng O.
- Khoảng cách từ tâm O đến các tiêu điểm F1, F2 được gọi là bán tiêu cự (c).
- Các đỉnh của hình elip được ký hiệu là A1, A2, B1 và B2.
- Chiều dài của trục bé B1B2 là 2a.
- Chiều dài của trục lớn A1A2 là 2b.
- Tiêu cự của hình elip F1F2 có độ dài là 2c.
Tóm lại, các thành phần chính của hình elip bao gồm các đỉnh A1, A2, B1, B2, hai trục đối xứng A1A2 và B1B2, tâm đối xứng O, nửa chiều dài trục lớn (a), nửa chiều dài trục bé (b), và tiêu cự (c).
=> Công thức tính diện tích của một hình elip (ellipse) được cho bởi công thức sau:
Diện tích elip = π * a * b
Trong đó:
- π xấp xỉ 3.14159.
- a là độ dài của trục lớn (đường kính dài) của elip.
- b là độ dài của trục nhỏ (đường kính ngắn) của elip.

Phương trình chính tắc của elip
Phương trình chính tắc của elip được xác định bởi các thông tin về tiêu điểm, đỉnh trên trục lớn và các điểm đi qua. Để lập phương trình chính tắc của elip, ta sử dụng các công thức và thông tin sau:
- Tiêu điểm: F(Fx, Fy)
- Đỉnh trên trục lớn: A(Ax, Ay)
- Hai điểm đi qua: M(Mx, My) và N(Nx, Ny)
Phương trình chính tắc của elip có dạng:
[(x – Hx)^2 / a^2] + [(y – Ky)^2 / b^2] = 1
Trong đó:
- (Hx, Ky) là tọa độ của tâm elip.
- a là nửa chiều dài của trục lớn.
- b là nửa chiều dài của trục bé.
Để tìm các giá trị cụ thể của Hx, Ky, a và b, ta sử dụng các thông tin đã cho.
Ví dụ: Giả sử ta có tiêu điểm F(-2, 0), đỉnh trên trục lớn A(3, 0) và điểm đi qua M(0, 1) và N(1, √3/2).
- Tìm tâm elip (Hx, Ky): Tọa độ tâm elip là trung điểm giữa tiêu điểm và đỉnh trên trục lớn: Hx = (Fx + Ax) / 2 = (-2 + 3) / 2 = 1/2 Ky = (Fy + Ay) / 2 = (0 + 0) / 2 = 0
- Tìm nửa chiều dài của trục lớn (a): a là nửa khoảng cách từ tâm elip đến đỉnh trên trục lớn: a = |Ax – Hx| = |3 – 1/2| = 5/2
- Tìm nửa chiều dài của trục bé (b): b là nửa chiều dài từ tâm elip đến một trong hai điểm đi qua trục bé (M hoặc N). Ví dụ, chọn điểm M(0, 1): b = |My – Ky| = |1 – 0| = 1
Kết hợp các giá trị đã tính được vào phương trình chính tắc của elip, ta có: [(x – 1/2)^2 / (5/2)^2] + [(y – 0)^2 / 1^2] = 1
Share >> Công Thức Và Bài Tập Tính Diện Tích Tam Giác Đều, Tam Giác Vuông
3 Ví dụ bài tập tính diện tích hình elip
Bài tập 1
Tính diện tích của một hình elip có trục lớn (đường kính dài) a = 6 và trục nhỏ (đường kính ngắn) b = 4.
Theo công thức đã đề cập, diện tích hình elip được tính bằng π * a * b.
Thay vào giá trị, ta có: a = 6 b = 4 π (Pi) có thể xấp xỉ 3.14159
Diện tích hình elip = π * 6 * 4
Sử dụng giá trị xấp xỉ của π (3.14159), ta có: Diện tích hình elip ≈ 3.14159 * 6 * 4 ≈ 75.39816
Bài tập 2
Lập phương trình chính tắc của elip (E) trong các trường hợp dưới đây:
- Một đỉnh trên trục lớn là (3; 0) và một tiêu điểm là (-2; 0)
- Elip (E) đi qua điểm M(0;1) và N(1, √3⁄2)
Phương pháp giải:
- Xác đinh được a nhờ một đỉnh trên trục lớn là A(2, 0) => a = 3.
- Xác đinh được c qua tiêu điểm là F(0, -3) => c = 2
- Có a, c => tính được b. b2 = a² – c2
- Để tính câu b, thì chỉ cần thay toạn độ M, N vào phương trinhg E
Giải
- Ta có: a = 3, c =2 => b² = a² – c² = 9 – 4 = 5.
=> Phương trình chính tắc của elip là: x²⁄9 + y²⁄5 = 1
- Phương trình chính tắc của (E) có dạng: x²⁄a² + y²⁄b²= 1
Vì E đi qua điểm M(0;1) và N(1, √3⁄2) nên thay tọa độ của M và N vào phương trình (E) ta được: x²⁄4 + y²⁄1 = 1
Bài tập 3
Giả sử ta có phương trình chính tắc của elip là [(x – 2)^2 / 9] + [(y – 1)^2 / 4] = 1. Hãy tính diện tích của hình elip này.
Bước 1: Xác định các thông số từ phương trình chính tắc:
- Tọa độ tâm elip là (Hx, Ky) = (2, 1).
- Nửa chiều dài của trục lớn là a = 3.
- Nửa chiều dài của trục bé là b = 2.
Bước 2: Tính diện tích hình elip:
- Diện tích = π * a * b = π * 3 * 2 = 6π.
Vậy, diện tích của hình elip được xác định bởi phương trình chính tắc [(x – 2)^2 / 9] + [(y – 1)^2 / 4] = 1 là 6π (đơn vị diện tích).
Xem thêm >> Hình chiếu góc vuông là gì? Cách vẽ hình chiếu góc vuông
Tạm kết
Trên đây là những kiến thức và Review Điện Thoại đã chia sẻ về hình elip, công thức và bái tập tính diện tích hình elip, phương trình chính tắc liên quan đến hình elip. Hy vọng bài viết hữu ích với các bạn!



