[Share] Công Thức Và Bài Tập Tính Diện Tích Tam Giác Đều, Tam Giác Vuông

Tam giác là một trong những hình học cơ bản của chương trình học cấp 1 và cấp 2. Cùng Review Điện Thoại ôn lại kiến thức về tam giác, công thức diện tích tam giác đều, tam giác vuông. Giải các bài tập công thức tính diện tích tam giác đều và tam giác vuông nhé!

Xem thêm >>  Hình Thang Cân Là Gì? Tính Chất Hình Thang Cân Là Gì? Tính Chu Vi Diện Tích Hình Thang Cân

Công thức diện tích tam giác đều

Ta có công thức tính diện tích của tam giác bất kỳ là:

Diện tích tam giác = (cạnh đáy x chiều cao) / 2

Trong đó, cạnh đáy là đoạn thẳng nối hai đỉnh của tam giác mà đỉnh thứ ba nằm trên đó, và chiều cao là đường thẳng vuông góc từ đỉnh của tam giác tới cạnh đáy hoặc phần tiếp tuyến của cạnh đáy.

Đối với tam giác đều, chiều cao cũng chính là đường trung tuyến, đường trung bình và đường phân giác của tam giác, và được tính bằng cạnh đáy nhân với căn hai chia cho hai. Vì cả ba cạnh của tam giác đều bằng nhau, ta có thể sử dụng công thức cụ thể hơn để tính diện tích tam giác đều là:

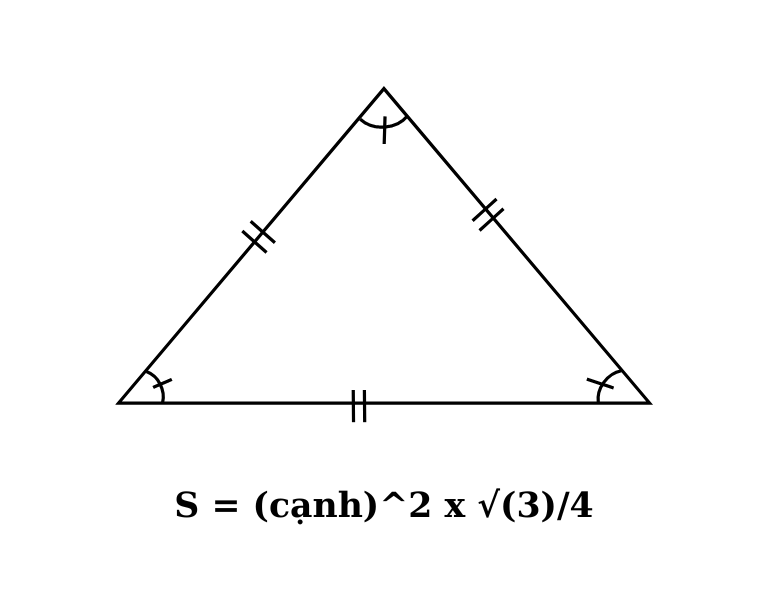
Diện tích tam giác đều = (cạnh)^2 x sqrt(3) / 4

Trong đó, sqrt(3) là căn bậc hai của số 3.

Với các bạn chưa học đến căn bậc hai, để giải những bài toán tính diện tích tam giác đều mà chưa có đường cao cho trước. Các bạn hãy tiến hành kẻ đường cao cho tam giác đều và áp dụng công thức chung khi tính diện tích tam giác: Diện tích tam giác = (cạnh đáy x chiều cao) / 2

Bài tập công thức diện tích tam giác đều

Bài tập 1

Hãy tính diện tích tam giác đều có cạnh bằng 6 cm.

• Giải:

Để tính diện tích tam giác đều, ta sử dụng công thức:

Diện tích tam giác đều = (cạnh)^2 x sqrt(3) / 4

Diện tích tam giác đều là:

6^2 x căn bậc hai của số 3 / 4 ≈ 15,59 cm^2

Đáp số: 15,59 cm^2 (làm tròn đến hai chữ số thập phân).

 

Bài tập 2

Cho tam giác đều ABC có cạnh bằng 8 cm và đường cao AH. Hãy tính diện tích tam giác đều ABC.

• Hướng dẫn

Với tam giác đều, ta có thể tính diện tích bằng công thức:

Diện tích tam giác đều = (cạnh)^2 x sqrt(3) / 4

Tuy nhiên, trong bài tập này chúng ta biết đường cao của tam giác đều, vì vậy ta có thể sử dụng công thức khác để tính diện tích:

Diện tích tam giác đều = (đường cao x cạnh đáy) / 2

• Giải

Trong tam giác đều, đường cao AH cũng là đường trung bình và đường trung trực của cạnh đáy BC.

Vậy nên, độ dài đường cao AH của tam giác ABC là:

AH = BC / 2 = 8 / 2 = 4 cm

Diện tích tam giác đều ABC là:

(4 x 8) / 2 = 16 cm^2

Đáp số: 16 cm^2.

Bài tập 3

Tính diện tích tam giác đều có độ dài cạnh bằng 10 cm.

• Hướng dẫn

Với tam giác đều, các cạnh bằng nhau nên ta có thể sử dụng công thức tính diện tích tam giác đều đơn giản: Diện tích tam giác đều = (cạnh)^2 x √3 / 4

• Giải

Diện tích của tam giác đều có độ dài cạnh bằng 10 cm là:

(10)^2 x √3 / 4 = 25√3 cm^2

Đáp số: 25√3 cm^2.

Share >> Công Thức Và Bài Tập Tính Chu Vi, Diện Tích Hình Vuông Có Lời Giải

Công thức tính diện tích tam giác vuông

Cách tính diện tích tam giác vuông đơn giản hơn tam giác đều vì cạnh vuông của tam giác vuông sẽ đồng thời làm đường cao của tam giác. Một trong những cách tính diện tích tam giác đều mà Review Điện Thoại hướng dẫn ở phía trên là phải kẻ thêm đường cao cho tam giác đều thì tam giác vuông không cần như thế.

Công thức tính diện tích tam giác vuông:

Diện tích tam giác vuông = (cạnh góc vuông thứ nhất) x (cạnh góc vuông thứ hai) / 2

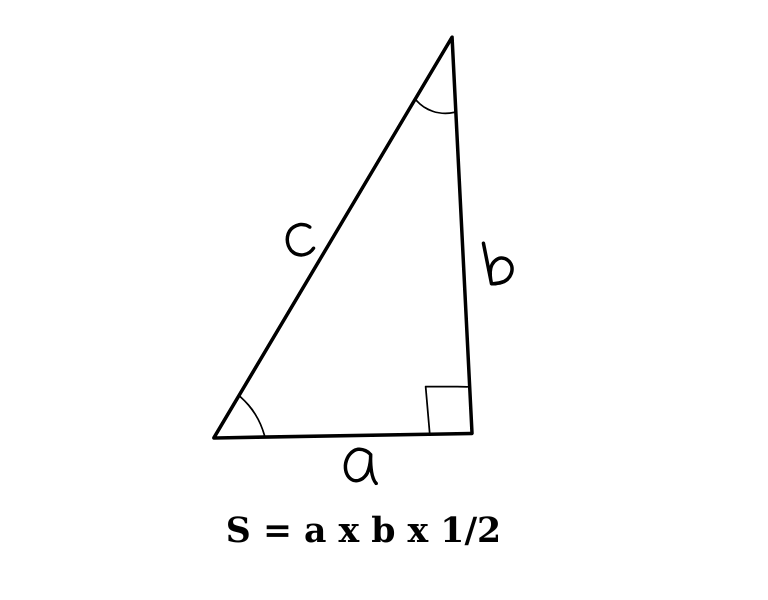
Bài tập tính diện tích tam giác vuông

Bài tập 1

Tam giác vuông DEF có hai cạnh góc vuông là DE = 6 cm và EF = 8 cm. Tính diện tích của tam giác vuông DEF.

• Giải

Áp dụng công thức tính diện tích tam giác vuông, ta có:

Diện tích = (cạnh góc vuông thứ nhất) x (cạnh góc vuông thứ hai) / 2

Với tam giác vuông DEF, hai cạnh góc vuông lần lượt là DE và EF, do đó ta có:

Diện tích tam giác vuông DEF là:

DE x EF / 2 = 6 x 8 / 2 = 24 cm^2

Đáp số: 24 cm^2.

 

Bài tập 2

Tam giác vuông XYZ có hai cạnh góc vuông là XZ = 10 cm và YZ = 24 cm. Tính diện tích của tam giác vuông XYZ.

• Giải

Áp dụng công thức tính diện tích tam giác vuông, ta có:

Diện tích = (cạnh góc vuông thứ nhất) x (cạnh góc vuông thứ hai) / 2

Với tam giác vuông XYZ, hai cạnh góc vuông lần lượt là XZ và YZ, do đó ta có:

Diện tích tam giác vuông XYZ là:

10 x 24 / 2 = 120 cm^2

Đáp số: 120 cm^2.

 

Bài tập 3

Tam giác vuông MNO có chu vi là 36 cm và độ dài cạnh huyền là 15 cm. Tính diện tích của tam giác vuông MNO.

• Giải

Ta biết rằng chu vi của tam giác vuông MNO là tổng độ dài các cạnh của tam giác:

Chu vi = MO + NO + MN = 15 + MO + NO

Do tam giác MNO là tam giác vuông nên ta có định lý Pythagoras:

MN^2 + NO^2 = MO^2

Vậy ta có hệ phương trình:

Chu vi = 15 + MO + NO MN^2 + NO^2 = MO^2

Thay NO = MO – 15 vào phương trình thứ nhất ta được:

Chu vi = 30 + MO

Thay NO = MO – 15 và MN^2 = MO^2 – NO^2 vào phương trình thứ hai ta được:

MO^2 – (MO – 15)^2 = MN^2 <=> 30MO – 225 = MN^2

Suy ra MO và MN:

• MO = (chu vi – 30) / 2
• MN = √[MO^2 – (MO – 15)^2]

Sau khi tính được độ dài của MO và MN, ta có thể tính diện tích của tam giác vuông MNO bằng công thức:

Diện tích = MO x MN / 2

Cuối cùng, các bạn chỉ cần thay số vào là ra nhé!

 Tìm hiểu >> Công Thức, Bài Tập Và Lời Giải Tính Chu Vi Và Diện Tích Hình Chữ Nhật