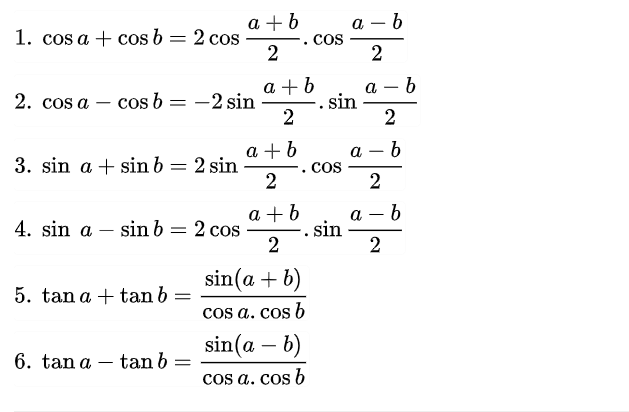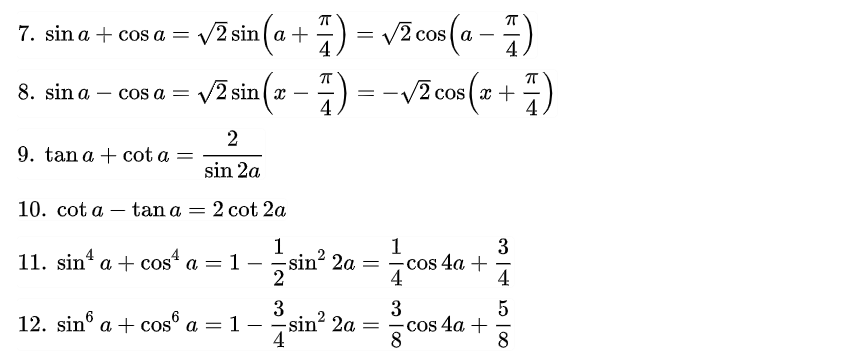Tổng Hợp Các Công Thức Lượng Giác Lớp 10 Từ Cơ Bản Đến Nâng Cao

Lượng giác là một trong những kiến thức toán học cơ bản nhất và cũng là quan trọng nhất của toán học lớp 10. Cùng Review Điện Thoại ôn lại tóm tắt các công thức lượng giác lớp 10 cơ bản nhé! Các công thức cộng lượng giác, công thức nhân hay các công thức hạ bậc… cùng bảng giá trị lượng giác một số góc đặc biệt.
Xem thêm >> Tổng Hợp 7 Hằng Đẳng Thức Đáng Nhớ Từ Cơ Bản Đến Nâng Cao Lớp 8, Lớp 9
Công thức lượng giác lớp 10 cơ bản
Công thức lượng giác cơ bản
Công thức cộng lượng giác
- Công thức cộng lượng giác cho sin:
sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
sin(a – b) = sin(a)cos(b) – cos(a)sin(b)
- Công thức cộng lượng giác cho cos:
cos(a + b) = cos(a)cos(b) – sin(a)sin(b)
cos(a – b) = cos(a)cos(b) + sin(a)sin(b)
- Từ công thức cộng lượng giác cho sin và cos, chúng ta có thể suy ra công thức cho tan:
tan(a + b) = [tan(a) + tan(b)] / [1 – tan(a)tan(b)]
tan(a – b) = [tan(a) – tan(b)] / [1 + tan(a)tan(b)]
Công thức các cung liên kết trên đường tròn lượng giác
- Hai góc đối nhau:
cos (-x) = cos x
sin (-x) = -sin x
tan (-x) = -tan x
cot (-x) = -cot x
- Hai góc bù nhau:
sin (π – x) = sin x
cos (π – x) = -cos x
tan (π – x) = -tan x
cot (π – x) = -cot x
- Hai góc phụ nhau:
sin (π/2 – x) = cos x
cos (π/2 – x) = sin x
tan (π/2 – x) = cot x
cot (π/2 – x) = tan x
- Hai góc hơn kém π:
sin (π + x) = -sin x
cos (π + x) = -cos x
tan (π + x) = tan x
cot (π + x) = cot x
- Hai góc hơn kém π/2:
sin (π/2 + x) = cos x
cos (π/2 + x) = -sin x
tan (π/2 + x) = -cot x
cot (π/2 + x) = -tan x
Công thức nhân
- Công thức nhân đôi:
sin2a = 2sina.cosa
cos2a = cos2a – sin2a = 2cos2a – 1 = 1 – 2sin2a
tan(2a) = [2tan(a)] / [1-tan^2(a)]
cot(2a) = [cot^2(a) – 1] / [2cot(a)]
- Công thức nhân ba:
sin(3a) = 3sin(a) – 4sin^3(a)
cos(3a) = 4cos^3(a) – 3cos(a)
tan(3a) = [3tan(a) – tan^3(a)] / [1 – 3tan^2(a)]
cot(3x) = [3 – cot^2(x)] / [3cot(x) – cot^3(x)]
- Công thức nhân bốn
sin(4x) = 2sin(2x)cos(2x) = 4sin(x)cos(x)[2cos²(x) – 1] = 8sin³(x)cos(x) – 4sin(x)cos(3x)
cos(4x) = cos²(2x) – sin²(2x) = 2cos²(2x) – 1 = 1 – 2sin²(2x) = 8cos⁴(x) – 8cos²(x) + 1 = 1 – 8sin²(x) + 8sin⁴(x)
tan(4x) = (4tan(x) – tan³(x)) / (1 – 6tan²(x) + tan⁴(x))
cot(4x) = (cot³(x) – 4cot(x)) / (3cot²(x) – 1)
Công thức hạ bậc
sin2a=1 – cos2a = 1 – (cos2a + 1)/2 = (1 – cos2a)/2.
cos2a = 1 – sin2a = (1 + cos2a)/2
tan2a = (1 – cos2a)/(1 + cos2a) = (2tan a)/(1 – tan2a)
cot2a = (1 + cos2a)/sin2a = (cot2a – 1)/2cot a
Công thức biến tổng thành tích
Đừng bỏ lỡ >> Hình Thang Cân Là Gì? Tính Chất Hình Thang Cân Là Gì? Tính Chu Vi Diện Tích Hình Thang Cân
Nghiệm phương trình lượng giác
- Phương trình lượng giác cơ bản
3. tan a= tan b⇔ a = b + kπ; (k ∈ Z)
4. cot a= cot b⇔ a = b + kπ; (k ∈ Z)
- Phương trình lượng giác trong trường hợp đặc biệt:
sin a = 0 ⇔ a = kπ; (k ∈ Z)
sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)
sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)
cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)
cos a = 1 ⇔ a = k2π; (k ∈ Z)
cos a = -1 ⇔ a = π + k2π; (k ∈ Z)
Bảng giá trị lượng giác một số góc đặc biệt
Share >> Công Thức, Bài Tập Và Lời Giải Tính Chu Vi Và Diện Tích Hình Chữ Nhật